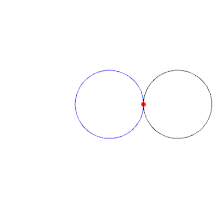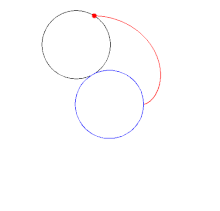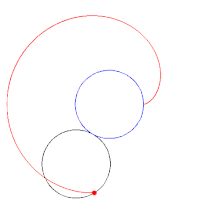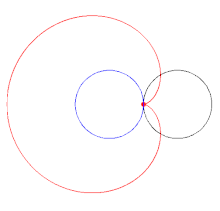
###### Created: 2023-11-13 14:45 ###### Areas & Topics: #mathematics ###### Note Type: #permanent ###### Connected to: [[]] 1. Imagine you have two identical coins placed end to end on one another. 2. Let’s call the top coin A and the bottom coin B. 3. Coin B is kept completely stationary, whilst Coin A is rolled around the circumference of Coin B, keeping a point of contact at all times (as in the image below). 4. Intuitively, you would expect that Coin A would make 1 revolution when going around Coin B (so a 360 degree turn) before returning to its starting position. 5. In actuality, Coin A makes 2 full revolutions (a 720 degree turn) before returning to its original position. Why is this? 1. This is because, whilst it looks like coin A is only travelling the distance of the circumference of coin B, the path it takes is actually that of a larger circle, meaning a larger circumference and thereby a further distance to travel. 2. This increased distance means that coin A makes 2 revolutions as opposed to 1 when both coins are of identical size (as the circumference of the bigger circle in this case will always be double that of either coin alone). 3. This longer path can be seen visually if you drew a line following the most outer point of coin A throughout its path travelling around coin B. 4. Simply put, imagine the big circle both coins are in, as opposed to the size of either coin alone, and you can see why the amount of revolutions needed is twice what you would expect.   ### Question Form ![[72157700983__A6C32908-BDF3-4996-BB9A-CA6341E9FB11.jpeg]] ### Resources https://en.m.wikipedia.org/wiki/Coin_rotation_paradox Einstein Puzzles - Dr. Gareth Moore